ГДЗ Геометрія 8 клас Мерзляк (2025)

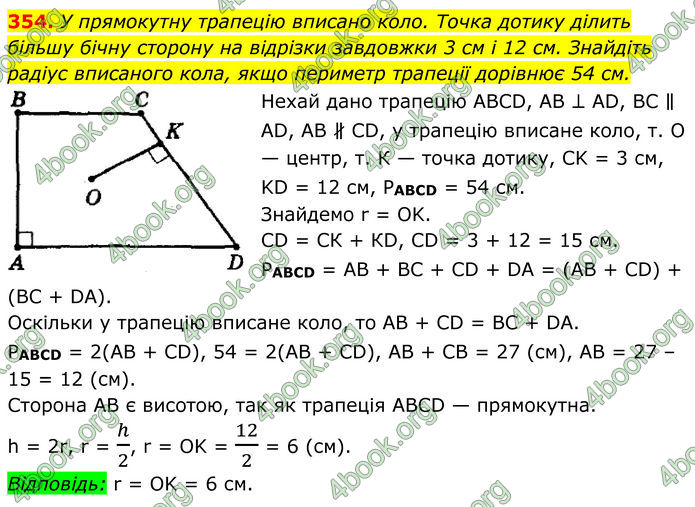
У прямокутну трапецію вписано коло. Точка дотику ділить більшу бічну сторону на відрізки завдовжки 3 см і 12 см. Знайдіть радіус вписаного кола, якщо периметр трапеції дорівнює 54 см.

Нехай дано трапецію АВСD, АВ ⊥ АD, ВС ∥ АD, АВ ∦ СD, у трапецію вписане коло, т. О — центр, т. К — точка дотику, СK = 3 см, KD = 12 см, РABCD = 54 см.
Знайдемо r = ОK. СD = СК + КD, СD = 3 + 12 = 15 см.
РABCD = АВ + ВС + СD + DА = (АВ + СD) + (ВС + DА).
Оскільки у трапецію вписане коло, то АВ + СD = ВС + DА. PABCD = 2(АВ + СD), 54 = 2(АВ + СD), АВ + СВ = 27 (см), АВ = 27 – 15 = 12 (см).
Сторона АВ є висотою, так як трапеція АВСD — прямокутна. h = 2r, r = h/2, r = OK = 12/2 = 6 (см).
Відповідь: r = ОK = 6 см.