ГДЗ Геометрія 8 клас Мерзляк (2025)

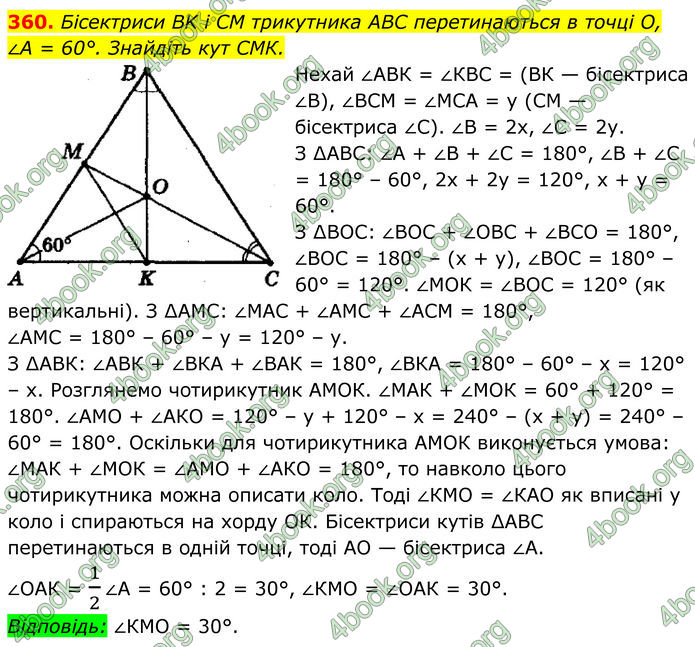
Бісектриси BK і CM трикутника ABC перетинаються в точці О, ∠A = 60°. Знайдіть кут СМК.

Нехай ∠АВК = ∠КВС = (ВК — бісектриса ∠В), ∠ВСМ = ∠МСА = у (СМ — бісектриса ∠С).
∠В = 2х, ∠С = 2у.
З ∆АВС: ∠А + ∠В + ∠С = 180°, ∠В + ∠С = 180° – 60°, 2х + 2у = 120°, х + у = 60°. З ∆ВОС: ∠ВОС + ∠ОВС + ∠ВСО = 180°, ∠ВОС = 180° – (х + у), ∠ВОС = 180° – 60° = 120°.
∠МОК = ∠ВОС = 120° (як вертикальні).
З ∆АМС: ∠МАС + ∠АМС + ∠АСМ = 180°, ∠АМС = 180° – 60° – у = 120° – у.
З ∆АВК: ∠АВК + ∠ВКА + ∠ВАК = 180°, ∠ВКА = 180° – 60° – х = 120° – х.
Розглянемо чотирикутник АМОК. ∠МАК + ∠МОК = 60° + 120° = 180°. ∠АМО + ∠АКО = 120° – у + 120° – х = 240° – (х + у) = 240° – 60° = 180°.
Оскільки для чотирикутника АМОК виконується умова: ∠МАК + ∠МОК = ∠АМО + ∠АКО = 180°, то навколо цього чотирикутника можна описати коло.
Тоді ∠КМО = ∠КАО як вписані у коло і спираються на хорду ОК.
Бісектриси кутів ∆АВС перетинаються в одній точці, тоді АО — бісектриса ∠А.
∠ОАК = 1/2∠А = 60° : 2 = 30°, ∠КМО = ∠ОАК = 30°.
Відповідь: ∠КМО = 30°.