ГДЗ Геометрія 8 клас Мерзляк (2025)

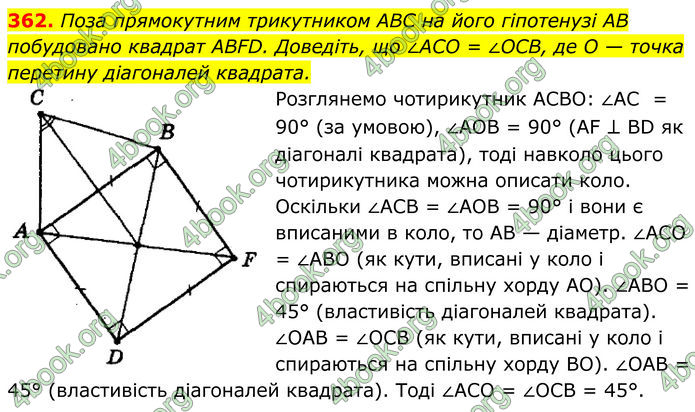
Поза прямокутним трикутником ABC на його гіпотенузі AB побудовано квадрат ABFD. Доведіть, що ∠ACO = ∠OCB, де O — точка перетину діагоналей квадрата.

Розглянемо чотирикутник АСВО: ∠АС = 90° (за умовою), ∠AОВ = 90° (AF ⊥ BD як діагоналі квадрата), тоді навколо цього чотирикутника можна описати коло.
Оскільки ∠АСВ = ∠АОВ = 90° і вони є вписаними в коло, то АВ — діаметр.
∠АСО = ∠АВО (як кути, вписані у коло і спираються на спільну хорду АО).
∠АВО = 45° (властивість діагоналей квадрата).
∠ОАВ = ∠ОСВ (як кути, вписані у коло і спираються на спільну хорду ВО).
∠ОАВ = 45° (властивість діагоналей квадрата). Тоді ∠АСО = ∠ОСВ = 45°.