ГДЗ Геометрія 8 клас Мерзляк (2025)

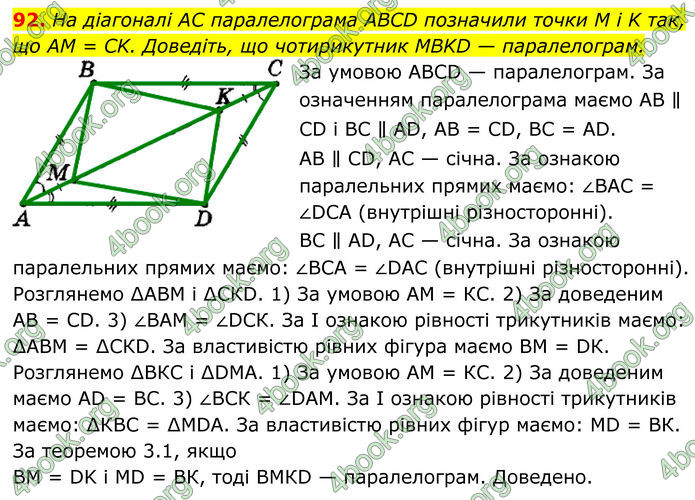
На діагоналі AC паралелограма ABCD позначили точки M і K так, що AM = CK. Доведіть, що чотирикутник MBKD — паралелограм.

За умовою АВСD — паралелограм. За означенням паралелограма маємо АВ ∥ СD і ВС ∥ АD, АВ = СD, ВС = АD. АВ ∥ СD, АС — січна. За ознакою паралельних прямих маємо: ∠ВАС = ∠DСА (внутрішні різносторонні). ВС ∥ АD, АС — січна. За ознакою паралельних прямих маємо: ∠ВСА = ∠DАС (внутрішні різносторонні). Розглянемо ∆АВМ і ∆СКD. 1) За умовою АМ = КС. 2) За доведеним АВ = СD. 3) ∠ВАМ = ∠DСК. За І ознакою рівності трикутників маємо: ∆АВМ = ∆СКD. За властивістю рівних фігура маємо ВМ = DК. Розглянемо ∆ВКС і ∆DМА. 1) За умовою АМ = КС. 2) За доведеним маємо АD = ВС. 3) ∠ВСК = ∠DАМ. За І ознакою рівності трикутників маємо: ∆КВС = ∆МDА. За властивістю рівних фігур маємо: МD = ВК. За теоремою 3.1, якщо ВМ = DK і МD = ВК, тоді ВМКD — паралелограм. Доведено.