ГДЗ Геометрія 8 клас Мерзляк (2025)

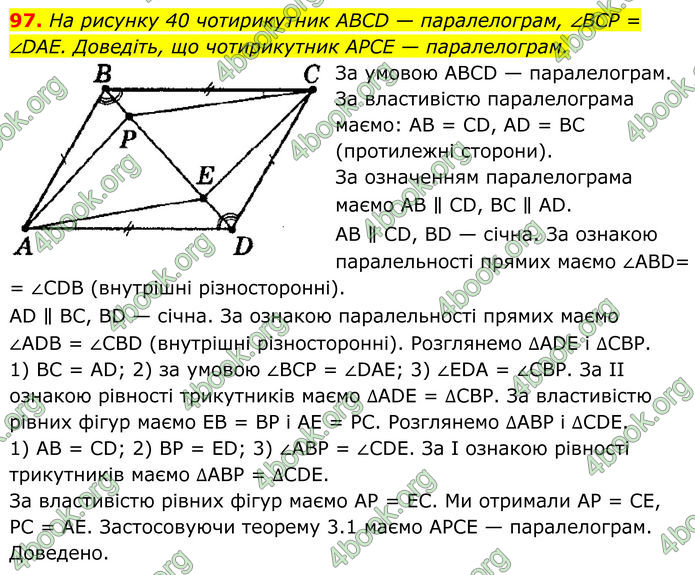
На рисунку 40 чотирикутник ABCD — паралелограм, ∠BCP = ∠DAE. Доведіть, що чотирикутник APCE — паралелограм.

За умовою АВСD — паралелограм. За властивістю паралелограма маємо: АВ = СD, АD = ВС (протилежні сторони). За означенням паралелограма маємо АВ ∥ СD, ВС ∥ АD. АВ ∥ СD, ВD — січна. За ознакою паралельності прямих маємо ∠АВD= = ∠СDВ (внутрішні різносторонні). АD ∥ ВС, ВD — січна. За ознакою паралельності прямих маємо ∠АDВ = ∠СВD (внутрішні різносторонні). Розглянемо ∆АDЕ і ∆СВР. 1) ВС = АD; 2) за умовою ∠ВСР = ∠DАЕ; 3) ∠ЕDА = ∠СВР. За II ознакою рівності трикутників маємо ∆АDЕ = ∆СВР. За властивістю рівних фігур маємо ЕВ = ВР і АЕ = РС. Розглянемо ∆АВР і ∆СDЕ. 1) АВ = СD; 2) ВР = ЕD; 3) ∠АВР = ∠СDЕ. За І ознакою рівності трикутників маємо ∆АВР = ∆CDE. За властивістю рівних фігур маємо АР = ЕС. Ми отримали АР = СЕ, РС = АЕ. Застосовуючи теорему 3.1 маємо АРСЕ — паралелограм. Доведено.