ГДЗ Геометрія 8 клас Мерзляк (2025)

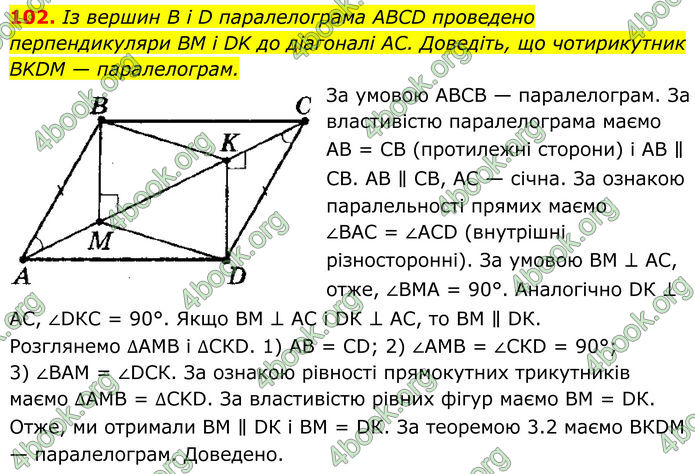
Із вершин B i D паралелограма ABCD проведено перпендикуляри BM і DK до діагоналі AC. Доведіть, що чотирикутник BKDM — паралелограм.

За умовою АВСВ — паралелограм. За властивістю паралелограма маємо АВ = СВ (протилежні сторони) і АВ ∥ СВ. АВ ∥ СВ, АС — січна. За ознакою паралельності прямих маємо ∠ВАС = ∠АСD (внутрішні різносторонні). За умовою ВМ ⊥ АС, отже, ∠ВМА = 90°. Аналогічно DК ⊥ АС, ∠DКС = 90°. Якщо ВМ ⊥ АС і DК ⊥ АС, то ВМ ∥ DК. Розглянемо ∆АМВ і ∆СКD. 1) АВ = СD; 2) ∠АМВ = ∠СКD = 90°; 3) ∠ВАМ = ∠DСК. За ознакою рівності прямокутних трикутників маємо ∆АМВ = ∆CKD. За властивістю рівних фігур маємо ВМ = DК. Отже, ми отримали ВМ ∥ DК і ВМ = DК. За теоремою 3.2 маємо ВКDМ — паралелограм. Доведено.