ГДЗ Геометрія 8 клас Мерзляк (2025)

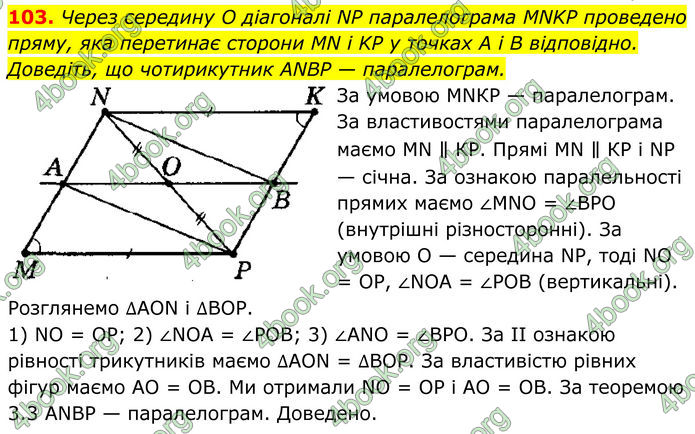
Через середину O діагоналі NP паралелограма MNKP проведено пряму, яка перетинає сторони MN і KP у точках A i B відповідно. Доведіть, що чотирикутник ANBP — паралелограм.

За умовою МNКР — паралелограм. За властивостями паралелограма маємо МN ∥ КР. Прямі МN ∥ КР і NР — січна. За ознакою паралельності прямих маємо ∠МNО = ∠ВРО (внутрішні різносторонні). За умовою О — середина NР, тоді NO = ОР, ∠NОА = ∠РОВ (вертикальні). Розглянемо ∆АON і ∆ВОР. 1) NO = ОР; 2) ∠NОА = ∠РОB; 3) ∠АNО = ∠ВРО. За II ознакою рівності трикутників маємо ∆АОN = ∆ВОР. За властивістю рівних фігур маємо АО = ОВ. Ми отримали NO = ОР і АО = ОВ. За теоремою 3.3 АNВР — паралелограм. Доведено.