ГДЗ Геометрія 8 клас Мерзляк (2025)

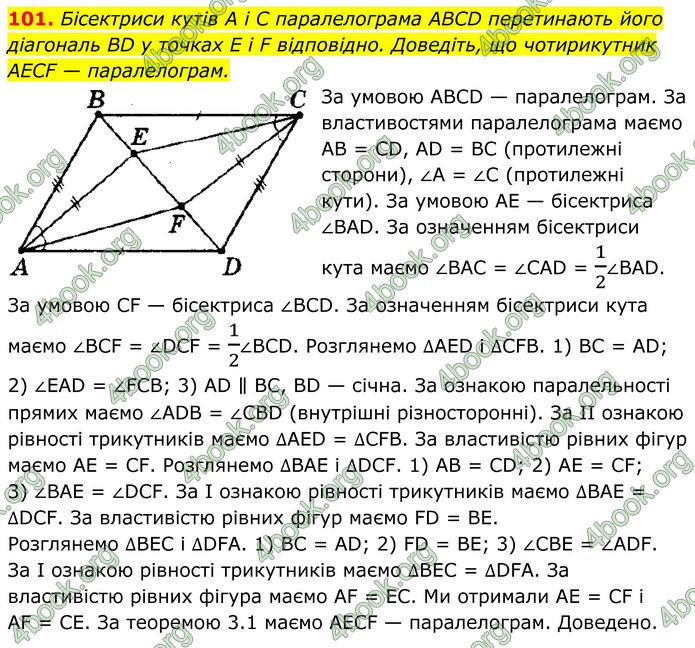
Бісектриси кутів A i C паралелограма ABCD перетинають його діагональ BD у точках E i F відповідно. Доведіть, що чотирикутник AECF — паралелограм.

За умовою АВСD — паралелограм. За властивостями паралелограма маємо АВ = СD, АD = ВС (протилежні сторони), ∠А = ∠С (протилежні кути). За умовою АЕ — бісектриса ∠ВАD. За означенням бісектриси кута маємо ∠ВАС = ∠САD = 1/2∠ВАD. За умовою СF — бісектриса ∠ВСD. За означенням бісектриси кута маємо ∠ВСF = ∠DСF = 1/2∠ВСD. Розглянемо ∆АЕD і ∆СFВ. 1) ВС = АD; 2) ∠ЕАD = ∠FСВ; 3) АD ∥ ВС, ВD — січна. За ознакою паралельності прямих маємо ∠АDВ = ∠СВD (внутрішні різносторонні). За II ознакою рівності трикутників маємо ∆АЕD = ∆СFВ. За властивістю рівних фігур маємо АЕ = СF. Розглянемо ∆ВАЕ і ∆DСF. 1) АВ = СD; 2) АЕ = СF; 3) ∠ВАЕ = ∠DСF. За І ознакою рівності трикутників маємо ∆ВАЕ = ∆DСF. За властивістю рівних фігур маємо FD = ВЕ. Розглянемо ∆ВЕС і ∆DFA. 1) ВС = АD; 2) FD = ВЕ; 3) ∠СВЕ = ∠АDF. За І ознакою рівності трикутників маємо ∆ВЕС = ∆DFА. За властивістю рівних фігура маємо АF = ЕС. Ми отримали АЕ = СF і АF = СЕ. За теоремою 3.1 маємо АEСF — паралелограм. Доведено.