ГДЗ Геометрія 8 клас Мерзляк (2025)

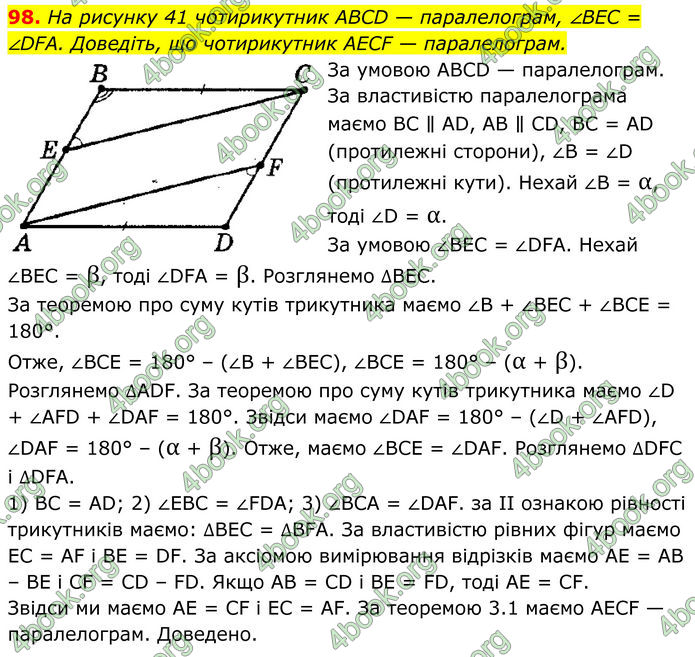
На рисунку 41 чотирикутник ABCD — паралелограм, ∠BEC = ∠DFA. Доведіть, що чотирикутник AECF — паралелограм. За умовою АВСD — паралелограм.

За властивістю паралелограма маємо ВС ∥ АD, АВ ∥ СD, ВС = АD (протилежні сторони), ∠В = ∠D (протилежні кути). Нехай ∠В = α, тоді ∠D = α. За умовою ∠ВЕС = ∠DFА. Нехай ∠ВЕС = β, тоді ∠DFА = β. Розглянемо ∆ВЕС. За теоремою про суму кутів трикутника маємо ∠В + ∠ВЕС + ∠ВСЕ = 180°. Отже, ∠ВСЕ = 180° – (∠В + ∠ВЕС), ∠ВСЕ = 180° – (α + β). Розглянемо ∆АDF. За теоремою про суму кутів трикутника маємо ∠D + ∠АFD + ∠DАF = 180°. Звідси маємо ∠DАF = 180° – (∠D + ∠АFD), ∠DАF = 180° – (α + β). Отже, маємо ∠ВСЕ = ∠DАF. Розглянемо ∆DFС і ∆DFА. 1) ВС = АD; 2) ∠ЕВС = ∠FDА; 3) ∠ВСА = ∠DАF. за II ознакою рівності трикутників маємо: ∆ВЕС = ∆ВFА. За властивістю рівних фігур маємо ЕС = АF і ВЕ = DF. За аксіомою вимірювання відрізків маємо АЕ = АВ – ВЕ і СF = СD – FD. Якщо АВ = СD і ВЕ = FD, тоді АЕ = СF. Звідси ми маємо АЕ = СF і ЕС = АF. За теоремою 3.1 маємо АЕСF — паралелограм. Доведено.