ГДЗ Геометрія 8 клас Мерзляк (2025)

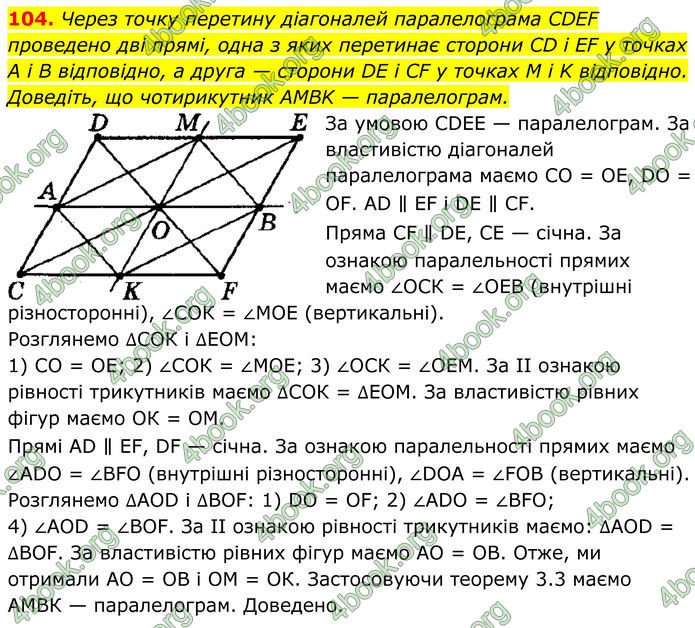
Через точку перетину діагоналей паралелограма CDEF проведено дві прямі, одна з яких перетинає сторони CD і EF у точках A i B відповідно, а друга — сторони DE і CF у точках M і K відповідно. Доведіть, що чотирикутник AMBK — паралелограм.

За умовою СDЕЕ — паралелограм. За властивістю діагоналей паралелограма маємо СО = ОЕ, DO = ОF. АD ∥ EF і DЕ ∥ СF. Пряма СF ∥ DЕ, СЕ — січна. За ознакою паралельності прямих маємо ∠ОСК = ∠ОЕВ (внутрішні різносторонні), ∠СОК = ∠МОЕ (вертикальні). Розглянемо ∆СОК і ∆ЕОМ: 1) СО = ОЕ; 2) ∠СОК = ∠МОЕ; 3) ∠ОСК = ∠ОЕМ. За II ознакою рівності трикутників маємо ∆СОК = ∆ЕОМ. За властивістю рівних фігур маємо ОК = ОМ. Прямі АD ∥ EF, DF — січна. За ознакою паралельності прямих маємо ∠АDО = ∠ВFО (внутрішні різносторонні), ∠DОА = ∠FОВ (вертикальні). Розглянемо ∆АОD і ∆ВОF: 1) DО = ОF; 2) ∠АDО = ∠ВFО; 4) ∠АОD = ∠ВОF. За II ознакою рівності трикутників маємо: ∆АОD = ∆ВОF. За властивістю рівних фігур маємо АО = ОВ. Отже, ми отримали АО = ОВ і ОМ = ОК. Застосовуючи теорему 3.3 маємо АМВК — паралелограм. Доведено.