ГДЗ Геометрія 8 клас Мерзляк (2025)

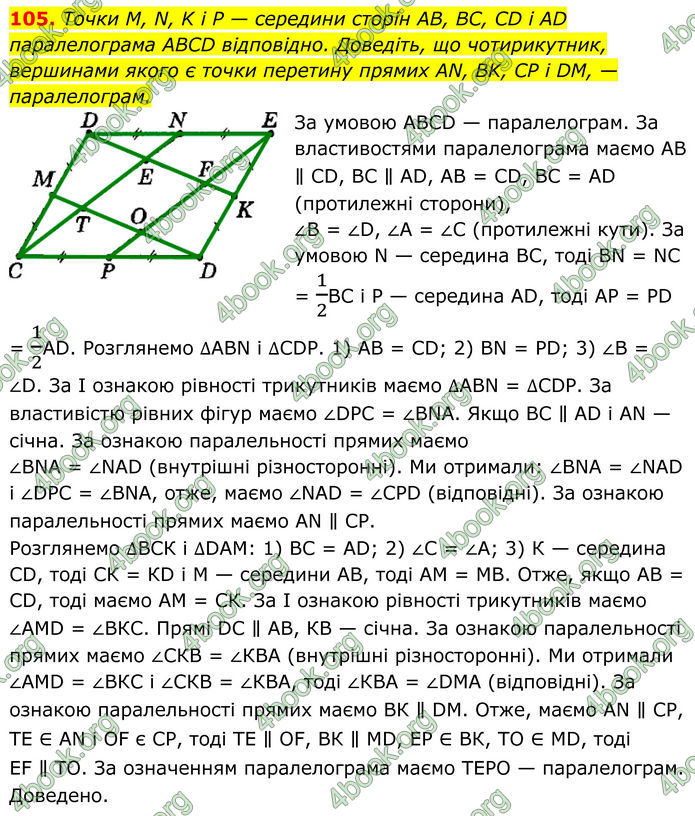
Точки M, N, K i P — середини сторін AB, BC, CD і AD паралелограма ABCD відповідно. Доведіть, що чотирикутник, вершинами якого є точки перетину прямих AN, BK, CP і DM, — паралелограм. За умовою АВСD — паралелограм.

За властивостями паралелограма маємо АВ ∥ СD, ВС ∥ АD, АВ = СD, ВС = АD (протилежні сторони), ∠В = ∠D, ∠А = ∠С (протилежні кути). За умовою N — середина ВС, тоді ВN = NС = 1/2ВС і Р — середина АD, тоді АР = РD = 1/2АD. Розглянемо ∆АВN і ∆СDР. 1) АВ = СD; 2) BN = РD; 3) ∠В = ∠D. За І ознакою рівності трикутників маємо ∆АВN = ∆СDР. За властивістю рівних фігур маємо ∠DРС = ∠ВNА. Якщо ВС ∥ АD і АN — січна. За ознакою паралельності прямих маємо ∠ВNА = ∠NAD (внутрішні різносторонні). Ми отримали: ∠ВNA = ∠NAD і ∠DРС = ∠ВNА, отже, маємо ∠NАD = ∠СРD (відповідні). За ознакою паралельності прямих маємо АN ∥ СР. Розглянемо ∆ВСК і ∆DАМ: 1) ВС = АD; 2) ∠С = ∠А; 3) К — середина СD, тоді СК = КD і М — середини АВ, тоді АМ = МВ. Отже, якщо АВ = СD, тоді маємо АМ = СК. За І ознакою рівності трикутників маємо ∠АМD = ∠ВКС. Прямі DС ∥ АВ, КВ — січна. За ознакою паралельності прямих маємо ∠СКВ = ∠КВА (внутрішні різносторонні). Ми отримали ∠АМD = ∠ВКС і ∠СКВ = ∠КВА, тоді ∠КВА = ∠DМА (відповідні). За ознакою паралельності прямих маємо ВК ∥ DМ. Отже, маємо AN ∥ СР, ТЕ ∈ АN і ОF є СР, тоді ТЕ ∥ ОF, ВК ∥ МD, ЕР ∈ ВК, ТО ∈ МD, тоді ЕF ∥ ТО. За означенням паралелограма маємо ТЕРО — паралелограм. Доведено.