Назад
ГДЗ Геометрія 8 клас Бурда (2025)
РОЗДІЛ 3. Подібність трикутників
Реклама:
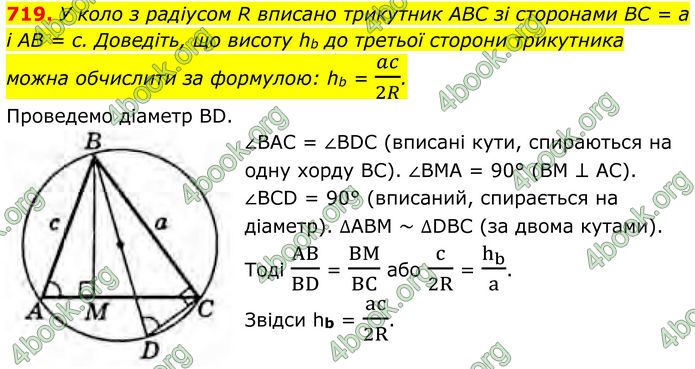
719. У коло з радіусом R вписано трикутник ABC зі сторонами BC = а і AB = с. Доведіть, що висоту hb до третьої сторони трикутника можна обчислити за формулою: hb = ac/2R.
Проведемо діаметр BD.
∠ВАС = ∠BDC (вписані кути, спираються на одну хорду BC).
∠BMA = 90° (ВМ ⊥ АС). ∠BCD = 90° (вписаний, спирається на діаметр).
∆АВМ ~ ∆DBC (за двома кутами).
Тоді AB/BD = BM/BC aбо c/2R = h_b/a. Звідси hb = ac/2R.






