ГДЗ Геометрія 7 клас Мерзляк (2024)

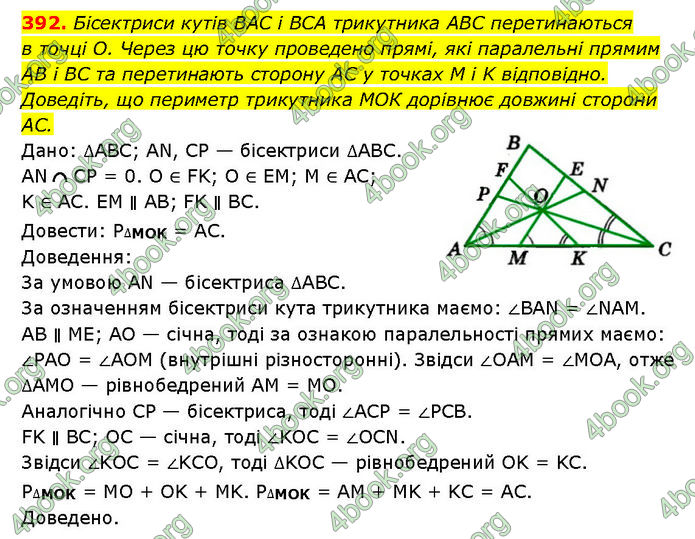
Бісектриси кутів ВАС і BCA трикутника ABC перетинаються в точці О. Через цю точку проведено прямі, які паралельні прямим AB і BC та перетинають сторону AC у точках M i K відповідно. Доведіть, що периметр трикутника МОК дорівнює довжині сторони AC.

Дано: ∆АВС; AN, CP — бісектриси ∆АВС. AN CP = 0. O ∈ FK; O ∈ EМ; M ∈ AC; K ∈ AC. ЕМ ∥ АВ; FK ∥ BC.
Довести: P∆MOK = AC.
Доведення: За умовою AN — бісектриса ∆АВС. За означенням бісектриси кута трикутника маємо: ∠BAN = ∠NAM. AB ∥ ME; AO — січна, тоді за ознакою паралельності прямих маємо: ∠PAO = ∠AOM (внутрішні різносторонні). Звідси ∠OAM = ∠MOA, отже ∆AMO — рівнобедрений AM = MO. Аналогічно CP — бісектриса, тоді ∠ACP = ∠PCB. FK ∥ BC; OC — січна, тоді ∠KOC = ∠OCN. Звідси ∠KOC = ∠KCO, тоді ∆KOC — рівнобедрений OK = KC. P∆MOK = МО + OK + MK. P∆MOK = AM + MK + KC = AC. Доведено.