ГДЗ Геометрія 7 клас Мерзляк (2024)

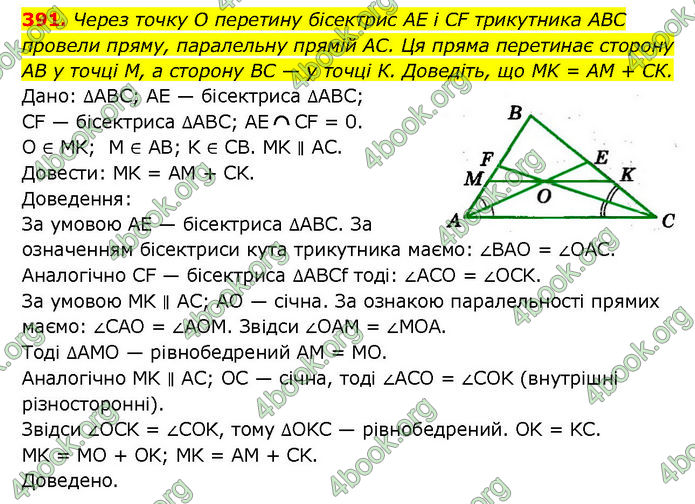
Через точку O перетину бісектрис AE і CF трикутника ABC провели пряму, паралельну прямій AC. Ця пряма перетинає сторону AB у точці М, а сторону BC — у точці К. Доведіть, що MK = AM + СК.

Дано: ∆ABC; AE — бісектриса ∆АВС; CF — бісектриса ∆АВС; AE CF = 0. O ∈ MK; M ∈ AB; K ∈ CB. MK ∥ AC. Довести: MK = AM + СK.
Доведення: За умовою AE — бісектриса ∆АВС. За означенням бісектриси кута трикутника маємо: ∠BAO = ∠OAC. Аналогічно CF — бісектриса ∆ABCf тоді: ∠ACO = ∠OCK. За умовою MK ∥ AC; AO — січна. За ознакою паралельності прямих маємо: ∠CAO = ∠AOM. Звідси ∠OAM = ∠MOA. Тоді ∆АМО — рівнобедрений AM = MO. Аналогічно MK ∥ AC; OC — січна, тоді ∠ACO = ∠COK (внутрішні різносторонні). Звідси ∠OCK = ∠COK, тому ∆ОKС — рівнобедрений. OK = KC. MK = MO + OK; MK = AM + CK. Доведено.