ГДЗ Геометрія 7 клас Мерзляк (2024)

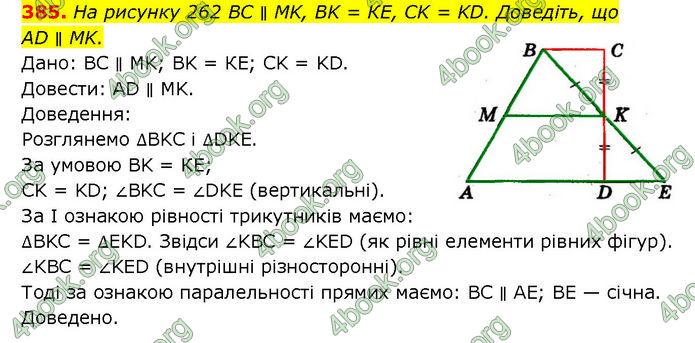
На рисунку 262 BC ∥ MK, BK = КЕ, CK = KD. Доведіть, що AD ∥ MK.

Дано: BC ∥ MK; BK = КЕ; CK = KD.
Довести: AD ∥ МK.
Доведення: Розглянемо ∆BKC і ∆DKE. За умовою BK = КЕ; CK = KD; ∠BKC = ∠DKE (вертикальні). За І ознакою рівності трикутників маємо: ∆BKC = ∆EKD. Звідси ∠KBC = ∠KED (як рівні елементи рівних фігур). ∠KBC = ∠KED (внутрішні різносторонні). Тоді за ознакою паралельності прямих маємо: BC ∥ AE; BE — січна. Доведено.