ГДЗ Геометрія 7 клас Мерзляк (2024)

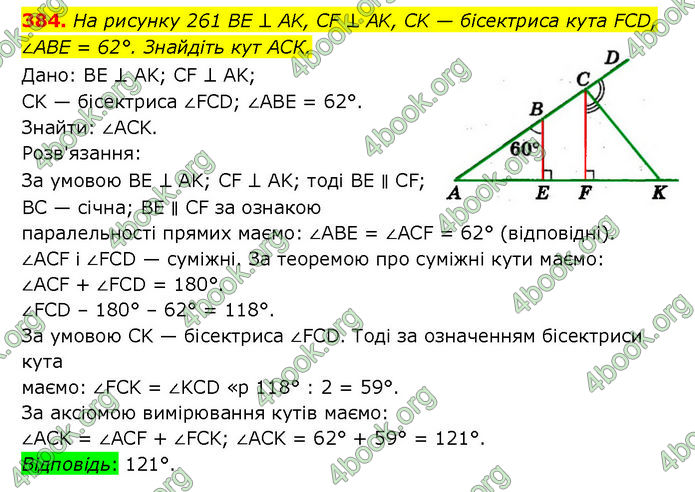
На рисунку 261 BE ⊥ AK, CF ⊥ AK, CK — бісектриса кута FCD, ∠ABE = 62°. Знайдіть кут АСК.

Дано: BE ⊥ AK; CF ⊥ AK; CK — бісектриса ∠FCD; ∠ABE = 62°.
Знайти: ∠ACK.
Розв'язання: За умовою BE ⊥ AK; CF ⊥ AK; тоді BE ∥ CF; BC — січна; BE ∥ CF за ознакою паралельності прямих маємо: ∠ABE = ∠ACF = 62° (відповідні). ∠ACF і ∠FCD — суміжні. За теоремою про суміжні кути маємо: ∠ACF + ∠FCD = 180°. ∠FCD – 180° – 62° = 118°. За умовою CK — бісектриса ∠FCD. Тоді за означенням бісектриси кута маємо: ∠FCK = ∠KCD «р 118° : 2 = 59°. За аксіомою вимірювання кутів маємо: ∠ACK = ∠ACF + ∠FCK; ∠ACK = 62° + 59° = 121°.
Відповідь: 121°.