ГДЗ Геометрія 7 клас Мерзляк (2024)

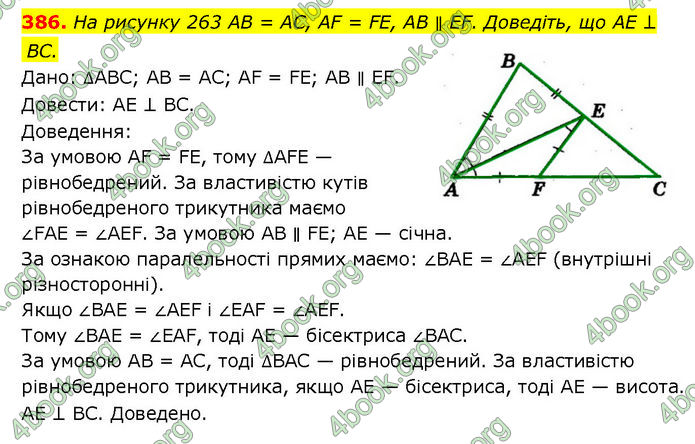
На рисунку 263 AB = AC, AF = FE, AB ∥ EF. Доведіть, що AE ⊥ BC.

Дано: ∆АВС; AB = AC; AF = FE; AB ∥ EF.
Довести: AE ⊥ BC.
Доведення: За умовою AF = FE, тому ∆AFE — рівнобедрений. За властивістю кутів рівнобедреного трикутника маємо ∠FAE = ∠AEF. За умовою AB ∥ FE; AE — січна. За ознакою паралельності прямих маємо: ∠BAE = ∠AEF (внутрішні різносторонні). Якщо ∠BAE = ∠AEF і ∠EAF = ∠AEF. Тому ∠BAE = ∠EAF, тоді AE — бісектриса ∠BAC. За умовою AB = AC, тоді ∆BAC — рівнобедрений. За властивістю рівнобедреного трикутника, якщо AE — бісектриса, тоді AE — висота. AE ⊥ BC. Доведено.