ГДЗ Геометрія 8 клас Бурда (2025)

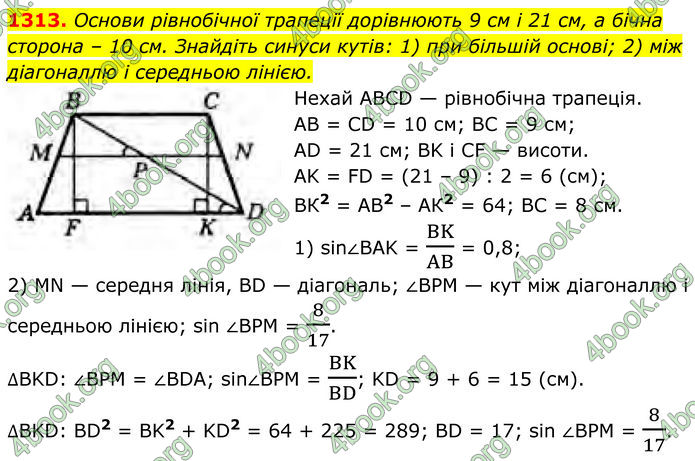
1313. Основи рівнобічної трапеції дорівнюють 9 см і 21 см, а бічна сторона – 10 см. Знайдіть синуси кутів: 1) при більшій основі; 2) між діагоналлю і середньою лінією.

Нехай ABCD — рівнобічна трапеція. AB = CD = 10 см; BC = 9 см; AD = 21 см; BK і CF — висоти.
AK = FD = (21 – 9) : 2 = 6 (см);
ВК2 = AВ2 – АК2 = 64; ВС = 8 см.
1) sin∠BAK = BK/AB = 0,8;
2) MN — середня лінія, BD — діагональ;
∠BPM — кут між діагоналлю і середньою лінією; sin ∠BPM = 8/17.
∆ВKD: ∠BPM = ∠BDA; sin∠BPM = BK/BD; KD = 9 + 6 = 15 (см).
∆BKD: BD2 = BK2 + KD2 = 64 + 225 = 289; BD = 17; sin ∠BPM = 8/17.