ГДЗ Геометрія 8 клас Бурда (2025)

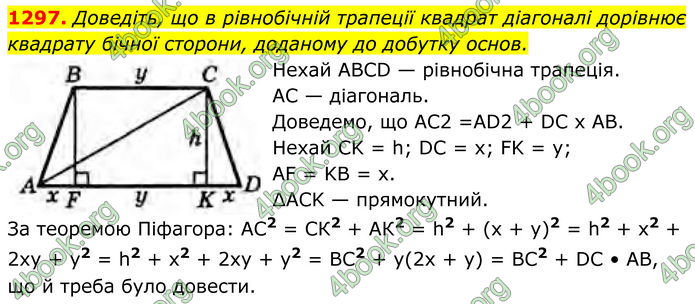
1297. Доведіть, що в рівнобічній трапеції квадрат діагоналі дорівнює квадрату бічної сторони, доданому до добутку основ.

Нехай ABCD — рівнобічна трапеція. AC — діагональ.
Доведемо, що АС2 =AD2 + DC x AB.
Hexaй CK = h; DC = x; FK = y; AF = KB = x.
∆ACK — прямокутний.
За теоремою Піфагора: АС2 = СК2 + АК2 = h2 + (x + у)2 = h2 + x2 + 2ху + y2 = h2 + x2 + 2ху + у2 = ВС2 + у(2х + у) = ВС2 + DC • AB, що й треба було довести.