ГДЗ Геометрія 8 клас Бевз (2025)

696. Доведіть геометрично нерівність: якщо a > 0 і b > 0, то (a+b)/2 ≥ √ab.

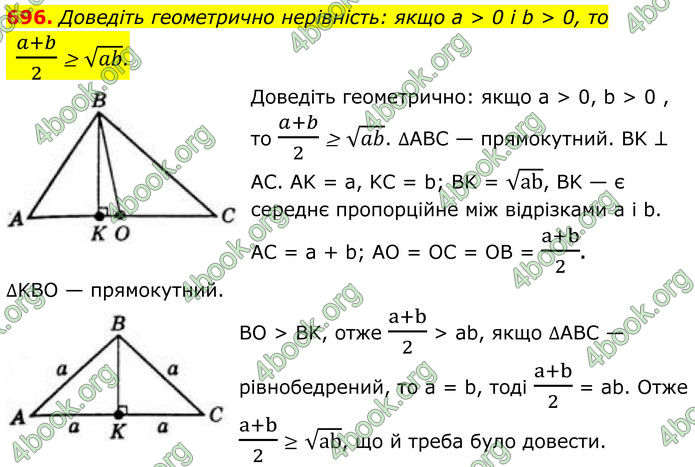
Доведіть геометрично: якщо а > 0, b > 0 , то (a+b)/2 ≥ √ab.
∆АВС — прямокутний. BK ⊥ AC.
AK = а, KC = b; BK = √ab, BK — є середнє пропорційне між відрізками а і b.
AC = а + b; AO = OC = OB = (a+b)/2. ∆KBO — прямокутний.
BO > BK, отже (a+b)/2 > аb, якщо ∆ABC — рівнобедрений, то а = b, тоді (a+b)/2 = аb.
Отже (a+b)/2 ≥ √ab, що й треба було довести.