ГДЗ Геометрія 7 клас Мерзляк (2024)

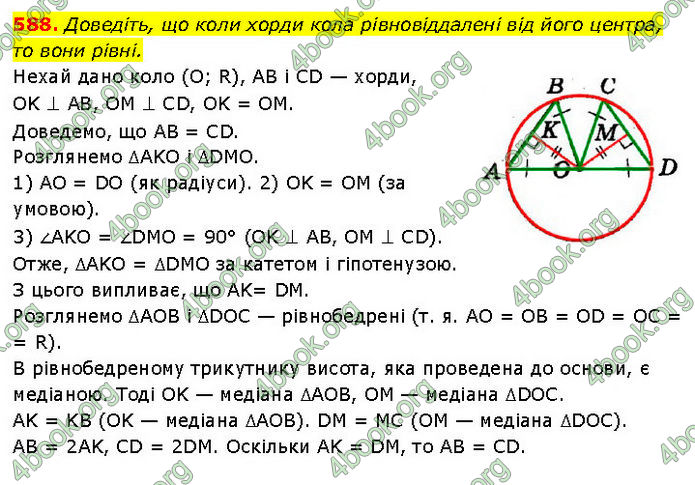
Доведіть, що коли хорди кола рівновіддалені від його центра, то вони рівні.

Нехай дано коло (О; R), AB і CD — хорди, OK ⊥ AB, OM ⊥ CD, OK = ОМ. Доведемо, що AB = CD. Розглянемо ∆AKO і ∆DMO. 1) AO = DO (як радіуси). 2) OK = OM (за умовою). 3) ∠AKO = ∠DMO = 90° (OK ⊥ AB, OM ⊥ CD). Отже, ∆AKO = ∆DMO за катетом і гіпотенузою. З цього випливає, що AK= DM. Розглянемо ∆AOB і ∆DOC — рівнобедрені (т. я. AO = OB = OD = OC = = R). В рівнобедреному трикутнику висота, яка проведена до основи, є медіаною. Тоді OK — медіана ∆AOB, OM — медіана ∆DOC. AK = KB (OK — медіана ∆AOB). DM = MC (ОМ — медіана ∆DOC). AB = 2AK, CD = 2DM. Оскільки AK = DM, то AB = CD.