ГДЗ Геометрія 8 клас Бевз (2025)

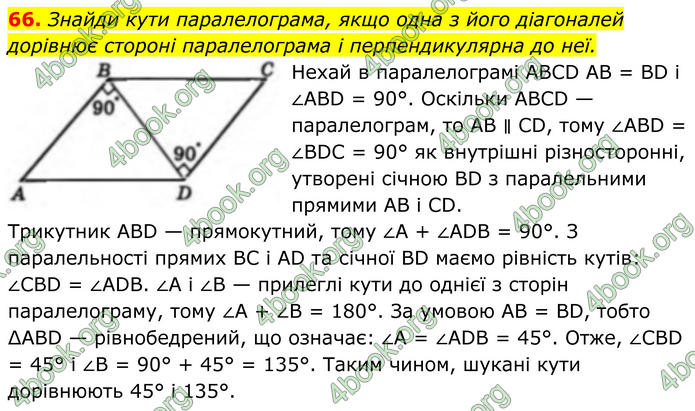
Знайди кути паралелограма, якщо одна з його діагоналей дорівнює стороні паралелограма і перпендикулярна до неї.

Нехай в паралелограмі ABCD AB = BD і ∠ABD = 90°. Оскільки ABCD — паралелограм, то AB ∥ CD, тому ∠ABD = ∠BDC = 90° як внутрішні різносторонні, утворені січною BD з паралельними прямими AB і CD. Трикутник ABD — прямокутний, тому ∠A + ∠ADB = 90°. З паралельності прямих BC і AD та січної BD маємо рівність кутів: ∠CBD = ∠ADB. ∠A і ∠B — прилеглі кути до однієї з сторін паралелограму, тому ∠A + ∠B = 180°. За умовою AB = BD, тобто ∆ABD — рівнобедрений, що означає: ∠A = ∠ADB = 45°. Отже, ∠CBD = 45° і ∠B = 90° + 45° = 135°. Таким чином, шукані кути дорівнюють 45° і 135°.