ГДЗ Геометрія 8 клас Бевз (2025)

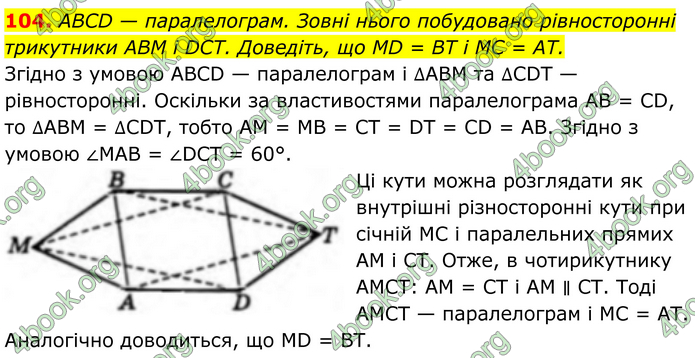
ABCD — паралелограм. Зовні нього побудовано рівносторонні трикутники ABM і DCT. Доведіть, що MD = BT і MC = AT.

Згідно з умовою ABCD — паралелограм і ∆ABM та ∆CDT — рівносторонні. Оскільки за властивостями паралелограма AB = CD, то ∆ABM = ∆CDT, тобто AM = MB = CT = DT = CD = AB. Згідно з умовою ∠MAB = ∠DCT = 60°. Ці кути можна розглядати як внутрішні різносторонні кути при січній MC і паралельних прямих AM і CT. Отже, в чотирикутнику AMCT: AM = CT і AM ∥ CT. Тоді AMCT — паралелограм і MC = AT. Аналогічно доводиться, що MD = BT.