ГДЗ Геометрія 8 клас Бевз (2025)

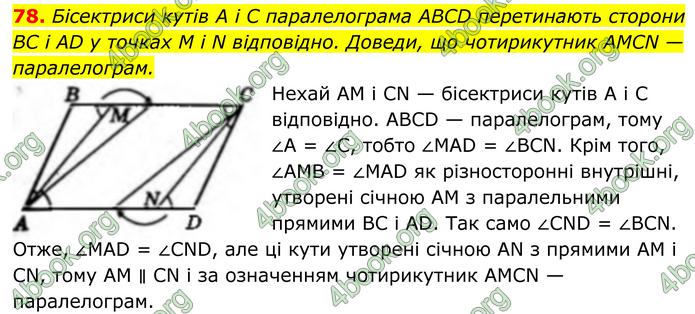
Бісектриси кутів A і C паралелограма ABCD перетинають сторони BC і AD у точках M і N відповідно. Доведи, що чотирикутник AMCN — паралелограм.

Нехай AM і CN — бісектриси кутів A і C відповідно. ABCD — паралелограм, тому ∠A = ∠C, тобто ∠MAD = ∠BCN. Крім того, ∠AMB = ∠MAD як різносторонні внутрішні, утворені січною AM з паралельними прямими BC і AD. Так само ∠CND = ∠BCN. Отже, ∠MAD = ∠CND, але ці кути утворені січною AN з прямими AM і CN, тому AM ∥ CN і за означенням чотирикутник AMCN — паралелограм.