ГДЗ Геометрія 8 клас Бевз (2025)

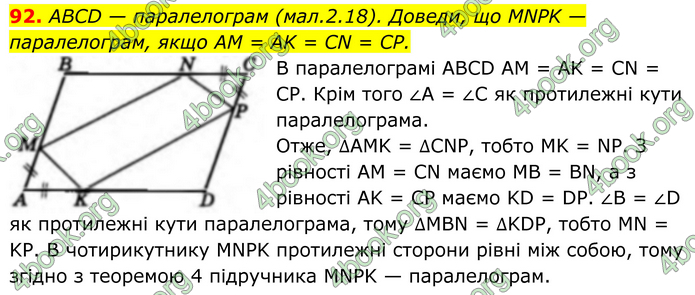
ABCD — паралелограм (мал.2.18). Доведи, що MNPK — паралелограм, якщо AM = AK = CN = CP. В паралелограмі ABCD AM = AK = CN = CP.

Крім того ∠A = ∠C як протилежні кути паралелограма. Отже, ∆AMK = ∆CNP, тобто MK = NP. З рівності AM = CN маємо MB = BN, а з рівності AK = CP маємо KD = DP. ∠B = ∠D як протилежні кути паралелограма, тому ∆MBN = ∆KDP, тобто MN = KP. В чотирикутнику MNPK протилежні сторони рівні між собою, тому згідно з теоремою 4 підручника MNPK — паралелограм.