ГДЗ Геометрія 8 клас Мерзляк (2025)

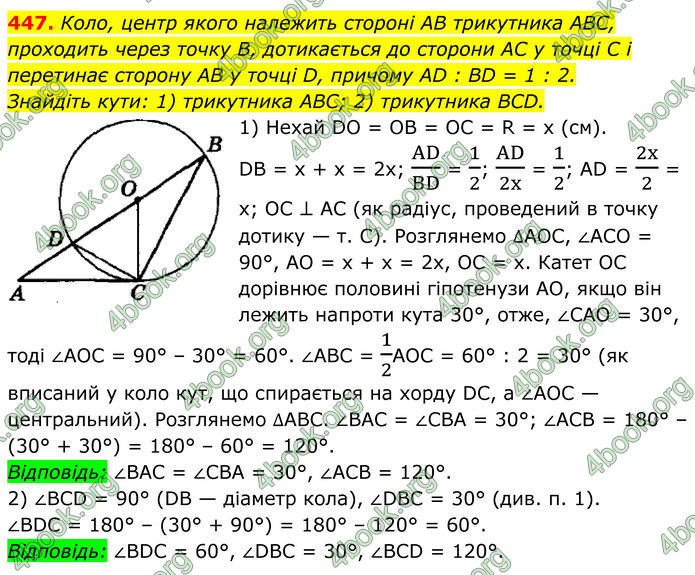
Коло, центр якого належить стороні AB трикутника ABC, проходить через точку В, дотикається до сторони AC у точці C і перетинає сторону AB у точці D, причому AD : BD = 1 : 2. Знайдіть кути: 1) трикутника ABC; 2) трикутника BCD.

1) Нехай DO = ОВ = ОС = R = х (см). DB = x + x = 2x; AD/BD = 1/2; AD/2x = 1/2; AD = 2x/2 = x; ОС ⊥ АС (як радіус, проведений в точку дотику — т. С).
Розглянемо ∆АОС, ∠ACO = 90°, АО = х + х = 2х, ОС = х.
Катет ОС дорівнює половині гіпотенузи АО, якщо він лежить напроти кута 30°, отже, ∠CAO = 30°, тоді ∠AOC = 90° – 30° = 60°.
∠АВС = 1/2АОС = 60° : 2 = 30° (як вписаний у коло кут, що спирається на хорду DС, a ∠AOC — центральний).
Розглянемо ∆АВС. ∠ВАС = ∠СВА = 30°; ∠ACB = 180° – (30° + 30°) = 180° – 60° = 120°.
Відповідь: ∠ВАС = ∠СВА = 30°, ∠АСВ = 120°.
2) ∠BCD = 90° (DB — діаметр кола), ∠DBC = 30° (див. п. 1).
∠BDC = 180° – (30° + 90°) = 180° – 120° = 60°.
Відповідь: ∠BDC = 60°, ∠DBC = 30°, ∠BCD = 120°.