ГДЗ Геометрія 8 клас Істер (2025)

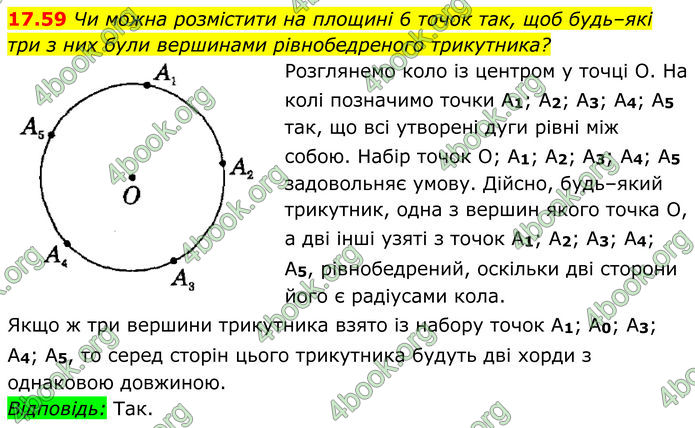
Чи можна розмістити на площині 6 точок так, щоб будь–які три з них були вершинами рівнобедреного трикутника?

Розглянемо коло із центром у точці О. На колі позначимо точки A1; A2; A3; A4; A5 так, що всі утворені дуги рівні між собою. Набір точок О; A1; A2; A3; A4; A5 задовольняє умову. Дійсно, будь–який трикутник, одна з вершин якого точка О, а дві інші узяті з точок A1; A2; A3; A4; A5, рівнобедрений, оскільки дві сторони його є радіусами кола. Якщо ж три вершини трикутника взято із набору точок A1; A0; A3; A4; A5, то серед сторін цього трикутника будуть дві хорди з однаковою довжиною.
Відповідь: Так.