Назад
ГДЗ Геометрія 8 клас Бурда (2025)
РОЗДІЛ 2. Чотирикутники
Реклама:
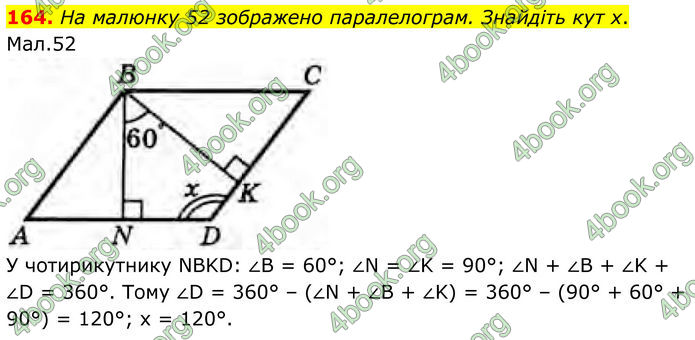
На малюнку 52 зображено паралелограм. Знайдіть кут х.
У чотирикутнику NBKD: ∠B = 60°; ∠N = ∠K = 90°; ∠N + ∠B + ∠K + ∠D = 360°. Тому ∠D = 360° – (∠N + ∠B + ∠K) = 360° – (90° + 60° + 90°) = 120°; x = 120°.






