ГДЗ Геометрія 8 клас Бурда (2025)

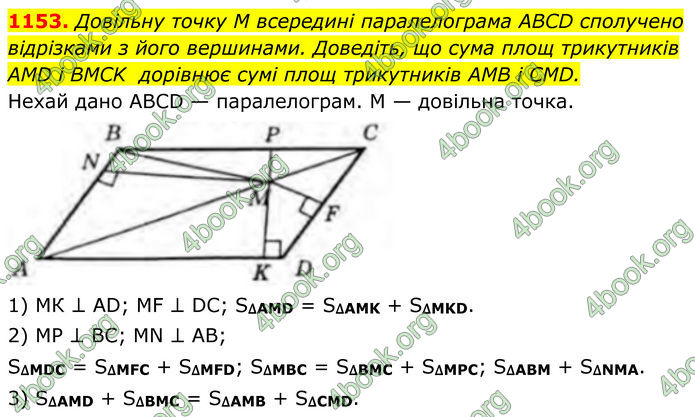
1153. Довільну точку M всередині паралелограма ABCD сполучено відрізками з його вершинами. Доведіть, що сума площ трикутників AMD і BMCK дорівнює сумі площ трикутників AMB і CMD.

Нехай дано ABCD — паралелограм. М — довільна точка.
1) МК ⊥ AD; MF ⊥ DC; S∆AMD = S∆AMK + S∆MKD.
2) MP ⊥ ВС; MN ⊥ AB; S∆MDC = S∆MFC + S∆MFD;
S∆MBC = S∆BMC + S∆MPC; S∆ABM + S∆NMA.
3) S∆AMD + S∆BMC = S∆AMB + S∆CMD.