ГДЗ Геометрія 7 клас Бевз (2024)

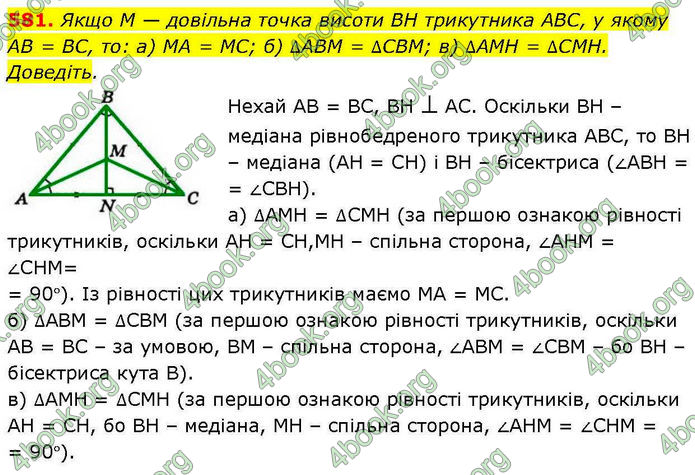
Якщо M — довільна точка висоти BH трикутника ABC, у якому AB = BC, то: a) MA = MC; б) ∆ABM = ∆CBM; в) ∆AMH = ∆CMH. Доведіть. 

Нехай АВ = ВС, ВН ⊥ АС. Оскільки ВН – медіана рівнобедреного трикутника АВС, то ВН – медіана (АН = СН) і ВН – бісектриса (∠АВН = ∠СВН).
а) ∆АМН = ∆СМН (за першою ознакою рівності трикутників, оскільки АН = СН,МН – спільна сторона, ∠АНМ = ∠СНМ = 90°).
Із рівності цих трикутників маємо МА = МС.
б) ∆АВМ = ∆СВМ (за першою ознакою рівності трикутників, оскільки АВ = ВС – за умовою, ВМ – спільна сторона, ∠АВМ = ∠СВМ – бо ВН – бісектриса кута В).
в) ∆АМН = ∆СМН (за першою ознакою рівності трикутників, оскільки АН = СН, бо ВН – медіана, МН – спільна сторона, ∠АНМ = ∠СНМ = 90°).