ГДЗ Геометрія 8 клас Бевз (2025)

Доведи, що довжина будь–якої сторони чотирикутника менша від суми довжин трьох інших його сторін.

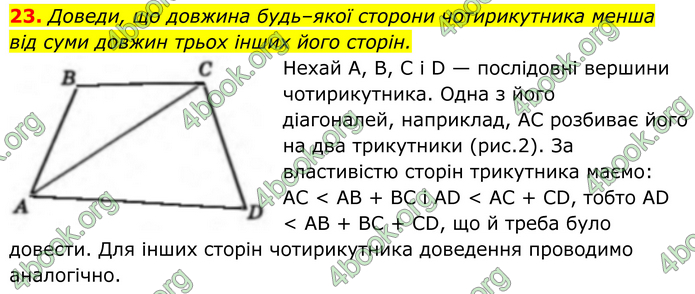
Нехай А, В, C і D — послідовні вершини чотирикутника. Одна з його діагоналей, наприклад, AC розбиває його на два трикутники (рис.2). За властивістю сторін трикутника маємо: AC < AВ + ВC і AD < AC + CD, тобто AD < AВ + BC + CD, що й треба було довести. Для інших сторін чотирикутника доведення проводимо аналогічно.