ГДЗ Геометрія 8 клас Істер (2025)

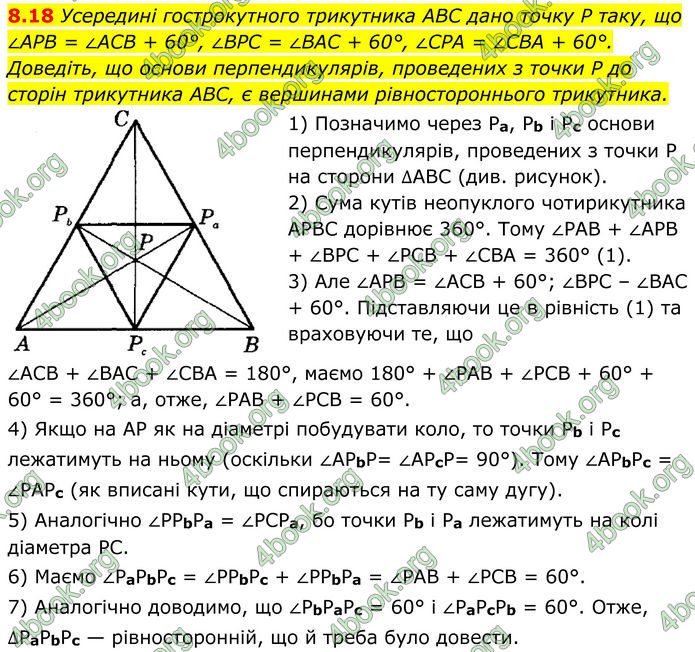
Усередині гострокутного трикутника ABC дано точку P таку, що ∠APB = ∠ACB + 60°, ∠BPC = ∠BAC + 60°, ∠CPA = ∠CBA + 60°. Доведіть, що основи перпендикулярів, проведених з точки P до сторін трикутника ABC, є вершинами рівностороннього трикутника.

1) Позначимо через Pa, Pb і Pc основи перпендикулярів, проведених з точки P на сторони ∆ABC (див. рисунок).
2) Сума кутів неопуклого чотирикутника APBC дорівнює 360°.
Тому ∠PAB + ∠APB + ∠BPC + ∠PCB + ∠CBA = 360° (1).
3) Але ∠APB = ∠ACB + 60°; ∠BPC – ∠BAC + 60°.
Підставляючи це в рівність (1) та враховуючи те, що ∠ACB + ∠BAC + ∠CBA = 180°, маємо 180° + ∠PAB + ∠PCB + 60° + 60° = 360°; а, отже, ∠PAB + ∠PCB = 60°.
4) Якщо на AP як на діаметрі побудувати коло, то точки Pb і Pc лежатимуть на ньому (оскільки ∠APbP= ∠APcP= 90°).
Тому ∠APbPc = ∠PAPc (як вписані кути, що спираються на ту саму дугу).
5) Аналогічно ∠PPbPa = ∠PCPa, бо точки Pb і Pa лежатимуть на колі діаметра PC.
6) Маємо ∠PaPbPc = ∠PPbPc + ∠PPbPa = ∠PAB + ∠PCB = 60°.
7) Аналогічно доводимо, що ∠PbPaPc = 60° і ∠PaPcPb = 60°.
Отже, ∆PaPbPc — рівносторонній, що й треба було довести.