ГДЗ Геометрія 7 клас Мерзляк (2024)

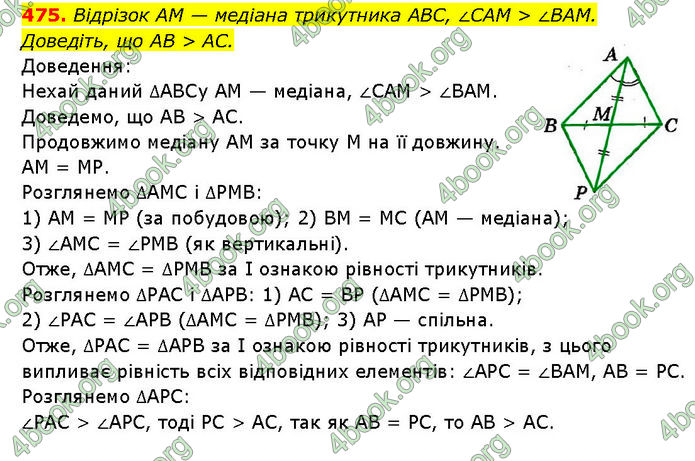
Відрізок AM — медіана трикутника ABC, ∠CAM > ∠BAM. Доведіть, що AB > AC.

Доведення:
Нехай даний ∆ABCy AM — медіана, ∠CAM > ∠BAM.
Доведемо, що AB > AC. Продовжимо медіану AM за точку M на її довжину. AM = MP.
Розглянемо ∆AMC і ∆PMВ: 1) AM = MP (за побудовою); 2) BM = MC (AM — медіана); 3) ∠AMC = ∠PMB (як вертикальні).
Отже, ∆AMC = ∆PMB за I ознакою рівності трикутників.
Розглянемо ∆PAC і ∆APB: 1) AC = BP (∆АМС = ∆PMВ); 2) ∠PAC = ∠APB (∆АМС = ∆PMB); 3) AP — спільна.
Отже, ∆PAC = ∆APB за І ознакою рівності трикутників, з цього випливає рівність всіх відповідних елементів: ∠APC = ∠BAM, AB = PC.
Розглянемо ∆АРС: ∠PAC > ∠APC, тоді PC > AC, так як AB = PC, то AB > AC.