ГДЗ Геометрія 7 клас Бурда

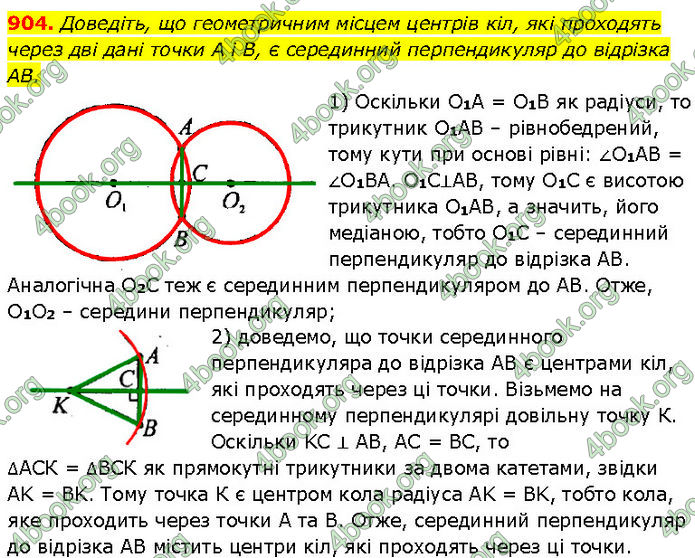
Доведіть, що геометричним місцем центрів кіл, які проходять через дві дані точки А і В, є серединний перпендикуляр до відрізка AB.

1) Оскільки О1А = О1В як радіуси, то трикутник О1AB – рівнобедрений, тому кути при основі рівні: ∠О1АВ = ∠О1ВА. О1С⊥AB, тому О1С є висотою трикутника О1AB, а значить, його медіаною, тобто О1С – серединний перпендикуляр до відрізка AB.
Аналогічна О2С теж є серединним перпендикуляром до AB. Отже, О1О2 – середини перпендикуляр;
2) доведемо, що точки серединного перпендикуляра до відрізка AB є центрами кіл, які проходять через ці точки. Візьмемо на серединному перпендикулярі довільну точку К.
Оскільки KC ⊥ AB, AC = BC, то ∆АСК = ∆ВСК як прямокутні трикутники за двома катетами, звідки AK = BK.
Тому точка К є центром кола радіуса AK = BK, тобто кола, яке проходить через точки A та В.
Отже, серединний перпендикуляр до відрізка AB містить центри кіл, які проходять через ці точки.