ГДЗ Геометрія 7 клас Бурда

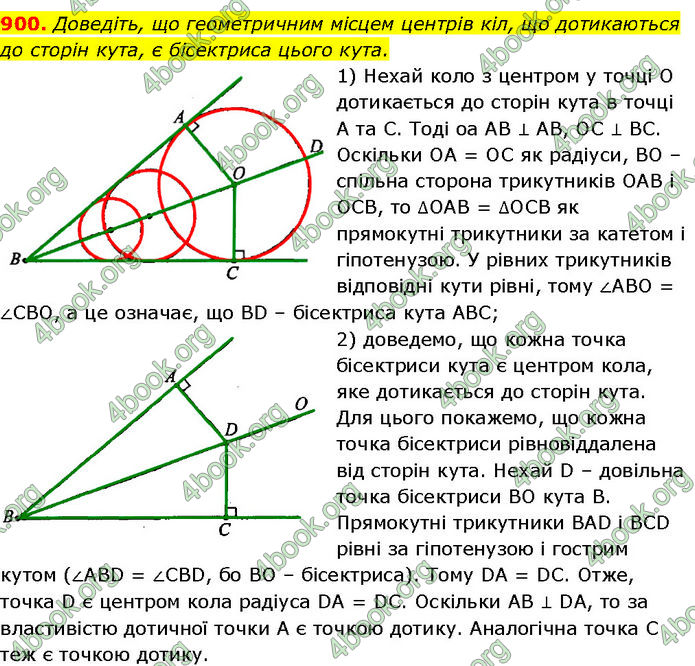
Доведіть, що геометричним місцем центрів кіл, що дотикаються до сторін кута, є бісектриса цього кута.

1) Нехай коло з центром у точці О дотикається до сторін кута в точці А та С. Тоді oa AB ⊥ АВ, ОС ⊥ BC.
Оскільки ОА = ОС як радіуси, BO – спільна сторона трикутників ОАВ і ОСВ, то ∆ОАВ = ∆ОСВ як прямокутні трикутники за катетом і гіпотенузою.
У рівних трикутників відповідні кути рівні, тому ∠АВО = ∠СВО, а це означає, що BD – бісектриса кута ABC;
2) доведемо, що кожна точка бісектриси кута є центром кола, яке дотикається до сторін кута. Для цього покажемо, що кожна точка бісектриси рівновіддалена від сторін кута.
Нехай D – довільна точка бісектриси BO кута В.
Прямокутні трикутники BAD і BCD рівні за гіпотенузою і гострим кутом (∠ABD = ∠CBD, бо BO – бісектриса).
Тому DA = DC. Oтже, точка D є центром кола радіуса DA = DC.
Oскільки AB ⊥ DA, то за властивістю дотичної точки А є точкою дотику. Aналогічна точка C теж є точкою дотику.