ГДЗ Геометрія 7 клас Бевз (2024)

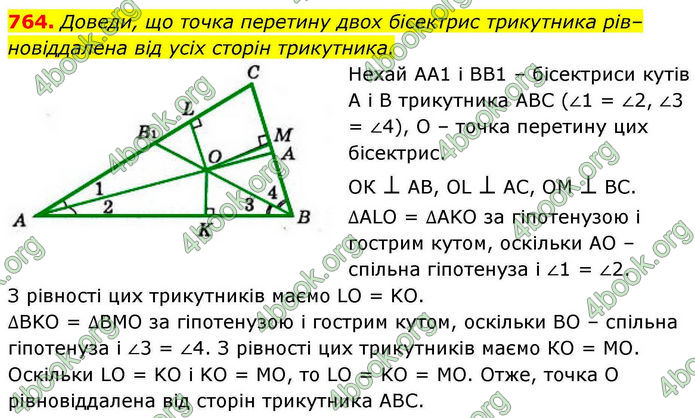
Доведи, що точка перетину двох бісектрис трикутника рівновіддалена від усіх сторін трикутника. 

Нехай АА1 і ВВ1 – бісектриси кутів А і В трикутника АВС (∠1 = ∠2, ∠3 = ∠4), О – точка перетину цих бісектрис.
ОК ⊥ АВ, OL ⊥ АС, ОМ ⊥ ВС. ∆ALO = ∆AKO за гіпотенузою і гострим кутом, оскільки АО – спільна гіпотенуза і ∠1 = ∠2.
З рівності цих трикутників маємо LO = KO.
∆BKO = ∆BMO за гіпотенузою і гострим кутом, оскільки ВО – спільна гіпотенуза і ∠3 = ∠4.
З рівності цих трикутників маємо КО = МО.
Оскільки LO = KO і KO = MO, то LO = KO = MO.
Отже, точка О рівновіддалена від сторін трикутника АВС.